Asker: Sanne, 16 years
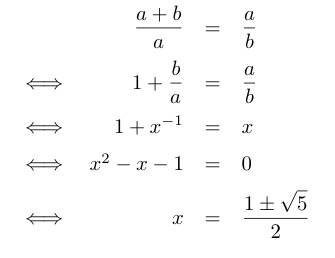
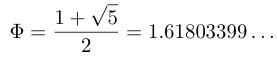
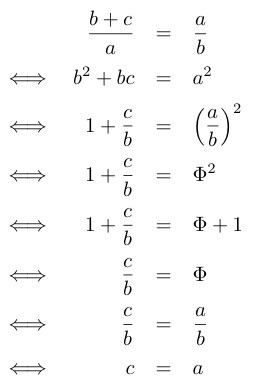


Answer
Dear Sanne,
A golden rectangle is a rectangle whose length to width is equal to the golden ratio

This Φ satisfies the property that Φ2=Φ+1 (just do the math).
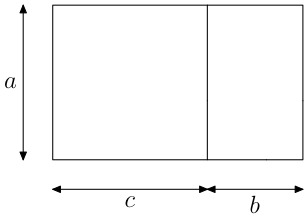
Suppose now that we add to a golden rectangle of length a and width b a rectangle of length a and width c so that we get a new golden rectangle of length b+c and width a.

We can now show that a must be equal to c and therefore that it is a square that we add to it.
We could do this as follows. Since both rectangles are similar, we get:

So we have shown:
If we add a rectangle to a golden rectangle so that we get a golden rectangle again, then the added rectangle must be a square.
Conversely, the statement also applies: If you have a rectangle that remains similar if you add a square to it, then it must be a golden rectangle.
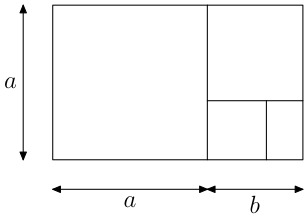
Take a look at the following figure:

If we add a rectangle with length a and width b to a square with side a, we get back a rectangle with length a+b and width a. If we want these rectangles to be similar, then (call x the ratio a/b):

The ratio must be positive, and we get that the rectangle that is similar if a square is added must have exactly (1+√5)/2 as its ratio.
As you can see in the figure, you can then also cut a square away from the smaller rectangle so that you get a golden rectangle again, etc.
With best regards,
Stijn Symens

Answered by
Dr. Stijn Symens
Math

University of Antwerp
Prinsstraat 13 2000 Antwerp
http://www.uantwerpen.be
Prinsstraat 13 2000 Antwerp
http://www.uantwerpen.be
.