How do I draw a right triangle given the acute angle and the radius of the inscribed circle?

Answer

Dear Stephen,

First of all, you should ask the teacher for additional explanations. The “I have a question” website can never replace a skilled subject teacher.

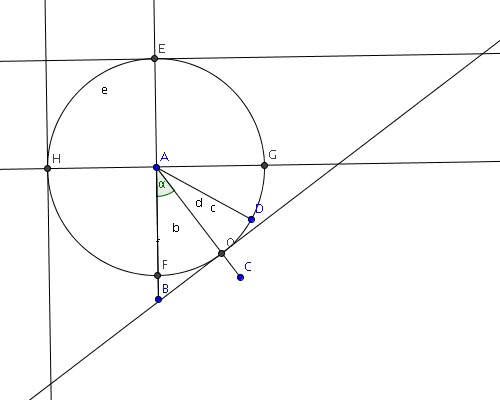
Below is a construction for the problem. It is best to view the different steps together in the attached figures. The solution below is only 1 possibility; maybe there are other and shorter methods…

Problem statement: given a segment and an angle, construct a right triangle of which the length of the radius of the inscribed circle is equal to the given segment and of which 1 of the angles is equal to the given angle.

Construction:
-Draw the circle with the given vertex as center and the given radius as radius.
-Extend one leg of the given angle and determine the opposite intersection with the circle. At that point of intersection, construct the tangent to the circle.
-Construct the perpendicular to the same leg of the given angle in the vertex. Determine the intersections with the circle and construct the tangent to the circle at one intersection.
-Construct the intersection of the other leg of the given angle with the circle and in that intersection construct the tangent to the circle.
-The intersections of the 3 tangents define a triangle that meets the requirements.

Note that no proof is given here that this construction is correct; after all, one still has to show that the triangle indeed meets all the conditions (for example, that it is a right triangle).

The attached drawings were made using the GeoGebra program.

Kind regards,
Peter Audenaert