My seven year old son would like to divide by infinity. How do you do that?

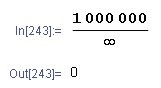
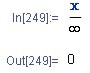
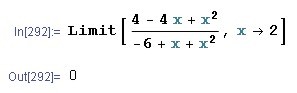
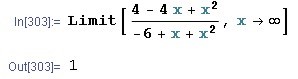
Answer

Dear Fabienne,

At first glance you would think. Why not?
If you divide any number by “a number that exceeds any other in size” – because that’s more or less how you can define the concept of infinity – you expect that the appropriate answer must always be 0. And yet your question also makes me curious.

Just to be sure (although… ) I gave it a try with Mathematica™, a powerful math suite on PC.

If you e.g. Divide 1000000 by infinity you will indeed get the answer zero from the program.

As long as you work purely numerically, there is no problem in itself, but if you consider what the answer must be to infinity divided by infinity, you immediately understand where things can go wrong. This quotient is indeed indefinite, and that’s the first reason why you can’t just divide by infinity. This exception can be very annoying, especially if you are going to work algebraically.

If we divide the variable x by infinity, then you can no longer predict the correct outcome of this operation. I was therefore unpleasantly surprised to find that Mathematica™ gives zero as an answer in this case. I honestly don’t agree with this dangerous answer. Because how can the program ever give me the previous answer “indefinite” afterwards if I replace (substitute) x with infinity afterwards?

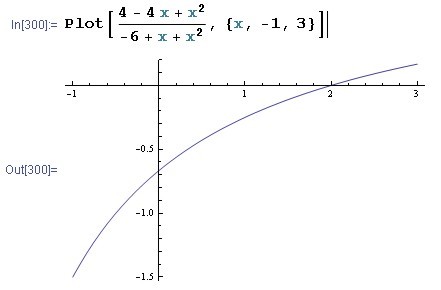
Inevitably, someone with some experience in mathematics will think of another application: limit calculations! A nice function to illustrate the problems that can arise with division by zero and/or infinity is eg. the function (4 – 4*x + x^2)/(-6 + x + x^2).

A graph of this function looks ordinary. Yet there is a problem:
for x going to 2, both the polynomial in the numerator and the polynomial in the denominator of the function become zero, and then the function actually becomes 0/0. This division is just as problematic as infinity divided by infinity. Actually there is a “hole” in the graph of the function at this place. In practice, of course, the plot command computes the function only for a limited number of values ​​of x, and therefore the computational environment “jumps” over the discontinuity.
In mathematics, such a function is called a retrievable discontinuity.
In this special case you can fill the “gap” neatly with the limit of the function for x going to 2.

The problem mentioned above already arises if you want to know where the function goes for very large x values: for x going to infinity, both the polynomial in the numerator and the polynomial in the denominator of the function become infinite, and then we are in first instance again with the indeterminacy. This time also the limit of the function for x going to infinity yields a finite answer. Mathematicians have an arsenal of techniques at their disposal to begin determining these kinds of limit values, and some of them are also provided in Mathematica™, including those for polynomial fractions. In this case we find a limit value of 1.

The problem with infinity is that apparently some sort of “pecking order of infinities” is needed somewhere to calculate correctly. One function goes to infinity faster than the other, and if you divide one by the other or vice versa, you arrive at zero in one case, and infinity in the other!

Last, but not least, most dangerous of all: depending on the application domain, mathematicians even use different versions of the concept of infinity.
When calculating with real numbers we distinguish between minus infinity and plus infinity,
whoever calculates with complex numbers actually has only one infinitely more.

Mathematica™ has provided the separate number ComplexInfinity for this.

In geometry, mathematicians prefer to use an infinite number of different oriented infinities (“infinitely far in a certain direction”). Mathematica™ has provided the separate number DirectedInfinity for this.

That’s why you have to be careful with “dividing by infinity” …