Does the direction of gravity always point to one point?

Answer

If you place a test mass near a mass distribution, for example in the shape of a banana, that banana will attract that mass. The point to which that force is directed depends on the shape of the body, and on the location of the test mass. As the test mass falls, the direction of the force will also change because the position of the test mass relative to the “parts” of the attracting mass is constantly changing.
So if you take several test masses and you place them stationary in a different place, the gauges that indicate the acceleration (and thus the direction of the force at that point) will not necessarily pass through the same point, or through the center of mass of the distribution.
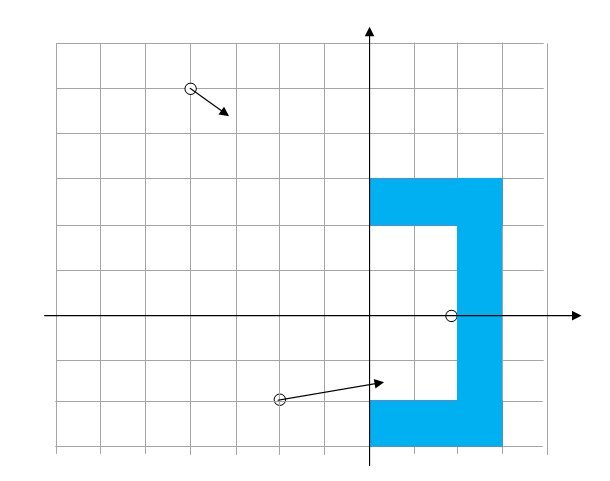
Look at the attached figure:
I took a 2-dimensional banana, made up of rectangles to keep things mathematically simple. A mass in the point (-4.5) experiences a force in the direction (0.146 , -0.101). The extension of that direction does not pass through the center of mass of the banana which is located at point (1.9 , 0) The reason is that the top part of the banana is closer to the test mass than the bottom one, so the mass is slightly more to pull in his direction. However, in the calculation of the center of mass, both pieces count equally.
At the bottom you see a 2nd test mass, whose acceleration is also indicated by an arrow. That arrow is also not aimed at the center of mass halfway the banana, but points a lot more horizontally due to the proximity of the bottom piece of banana.
So in every point in space you get an arrow that indicates the direction of gravity. All those arrows together represent the gravitational field of the banana. To calculate that pijenl you have to integrate the force over the attractive volume in each point via a double integral, (in 3 dimensions a 3-double integral) and that in each direction x, y and possibly z.