
Answer
Dear Emile
You have probably seen some properties of determinants? For example, subtract the first column from all the other columns, that doesn’t change the determinant.
.gif)
In the first row this produces the element a-(a+b) = -b. The diagonal elements become (a+b)-a = b and all other elements become aa = 0; so you get:

It is now obvious to make a lot of zeros in the first row: add all the other rows to that row, that does not change the determinant either. The first element of the first row was a+b and gets a total of n-1 times a, so it becomes na+b. The other elements in the first row are each added one b and thus become -b+b = 0; so you get:
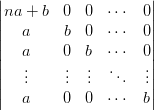
Here is the determinant of a triangle matrix, you might know that the determinant is equal to the product of the diagonal elements? If you don’t know that (yet), you can now also develop to the first row.
regards
Tom
Answered by
Tom Dorissen
Avenue des Pélain 2 1050 Ixelles
http://www.vub.ac.be/
.