Does a clock in a satellite that is further away from Earth tick slower because its speed is higher than the satellite that orbits closer to the Earth?

Answer

There are two effects that make the clock in a satellite differ from a clock on Earth.

– first, the satellite, for example ISS, moves opposite an observer on the Earth’s surface. That makes the clock in the satellite run slower than the one on Earth. This effect is therefore purely a consequence of the relative speed. But because the speed of a satellite (suppose a circular orbit so that it is constant) is unambiguously connected with the distance from the center of the earth, the time dilation can also be expressed as a function of that distance r . This is an effect from special relativity

– secondly, the earthling is closer to the center of the earth than the satellite. As a result, the terrestrial clock runs slower, or in other words: the satellite clock runs faster than the terrestrial clock. This effect is a result of gravity. Even if the satellite were to stand still in its orbit (which of course is not possible), this effect would remain. This effect is also a function of the distance to the center of the earth. This is an effect from general relativity.

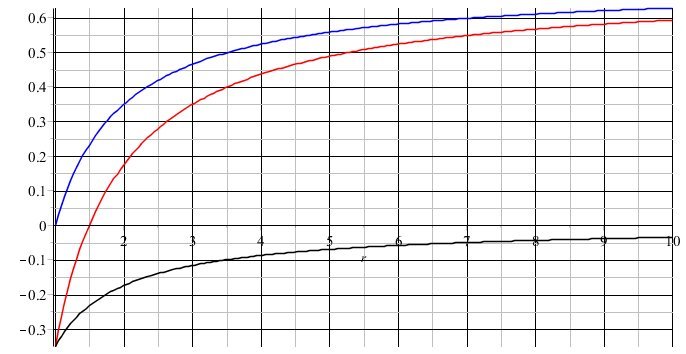
The two effects therefore work against each other but do not compensate each other. They both depend on the distance r from the center of the earth but in different ways. On the attached figure I have plotted the two effects and their sum. The horizontal axis is in Earth radii, so r = 1 is the Earth’s surface. The vertical axis shows in nanoseconds how much a clock in the satellite is behind or ahead of a clock on the Earth’s surface per second. So the unit on that axis is nanoseconds per second.

1) the bottom graph (black) shows the effect due to the speed. The lower the track, the higher the track speed (in m/s) and the greater this effect. At the height of the Earth’s surface, a clock in a satellite that skims just above the surface would run 0.35 nanoseconds slower per second. The effect goes to zero as the radius of the satellite orbit goes to infinity.

2) the top graph (blue) shows the effect of the Earth’s gravity. This difference in clock speed is zero in a satellite that would skim just above the Earth’s surface and then increases with altitude. The higher the orbit, the more the clock in the satellite is ahead of that on Earth.

The red graph shows the combination of both effects.

1) For circular orbits below 1.5 Earth radii (ie below 0.5 Earth radii in height) the effect of the speed predominates and the clock is net behind. Every year in the ISS an astronaut ‘gains’ roughly one hundredth of a second.

2) At 1.5 Earth radii, the two effects compensate each other and the clock in the satellite is synchronized with that on Earth.

3) Above that radius, the clock in the satellite runs faster than on Earth. There the effect is predominant due to gravity. This is the case, for example, for GPS satellites and for geostationary or geosynchronous satellites. An astronaut there would therefore age a little faster compared to a colleague on Earth.

For GPS satellites (at approximately r = 4), the clock in the satellite is about 38 microseconds a day ahead of a clock on Earth. This effect must be taken into account to achieve the desired accuracy of our GPS devices. No accurate GPS without general relativity!

See for example about the latter : http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/gps.html

and more generally the figure at: http://www.wired.com/2014/11/time-dilation/

Another important note: if two satellites in a circular orbit have the same period, they must also have orbits of equal radius. A specific radius belongs to a period and vice versa’ and thus also a specific orbital speed. For example, speed v and radius r are inextricably linked by the formula

v = square root (G Ma / r )

G is the universal gravitational constant and Ma is the mass of the Earth.

for the period this relation becomes : (2 pi / P) squared = G Ma /r3 (so r to the third)