Why is it that in balances the balance sometimes moves only moderately to the left and does not always deflect completely if, for example, the mass in the left shell is greater than the mass in the right shell?
I think a moment is exerted on the arms of the balance as long as there is a mass difference between the scales. The balance would then always have to deviate completely to the left with a (small) mass difference. Or am I making a mistake?
I can’t figure it out, any help is welcome!
Answer
Should the center of mass of the scale’s arms be at the center of rotation, you would be right.
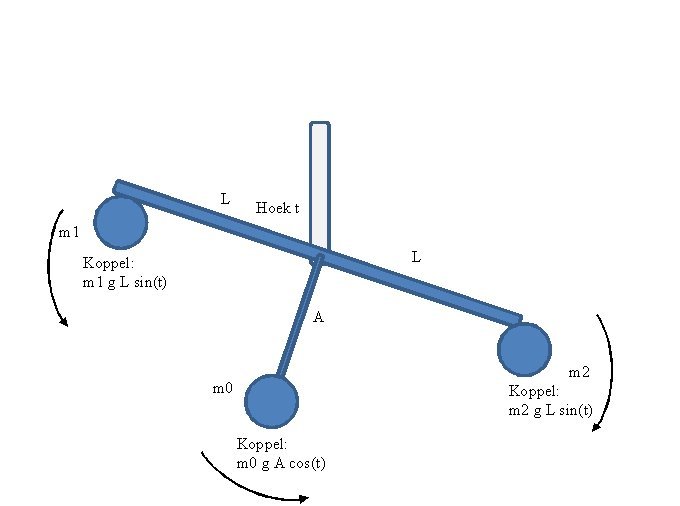
In a balance, the center of mass is lowered. Look at the attached figure: the center of mass is represented as an additional mass m0 on a vertical arm of length A, which is attached to the arms of the balance. In reality, m0 is incorporated in the shape of the arm piece.
Let t be the angle between the arm and the vertical. So t = 90° if the balance is balanced horizontally. If you now put a mass m1 on one side, and a larger mass m2 on the other side, the balance will go out of equilibrium. As a result, m0 will also output a torque, until equilibrium occurs:
m1 g L sin
(the cos
so the balance comes to rest at an angle cot
Since m0, L and A are known, the mass difference m1-m0 can be derived from the angle t.

Answered by
prof.dr. Paul Hellings
Department of Mathematics, Fac. IIW, KU Leuven

Old Market 13 3000 Leuven
https://www.kuleuven.be/
.